Private Attributes

BCGraphFitter Class Reference

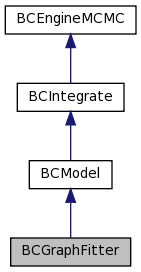
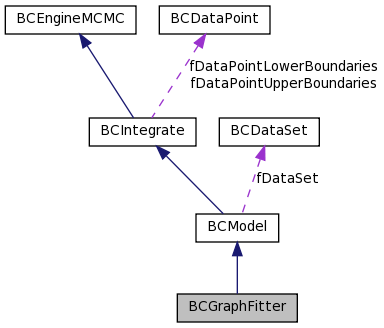
A class for fitting graphs with functions. More...

#include <BCGraphFitter.h>

Inheritance diagram for BCGraphFitter:
Inheritance graph
[legend]
Collaboration diagram for BCGraphFitter:
Collaboration graph
[legend]

List of all members.

Public Member Functions

Constructors and destructors

 BCGraphFitter ()
 BCGraphFitter (TGraphErrors *graph, TF1 *func)
 ~BCGraphFitter ()
Member functions (get)

TGraphErrors * GetGraph ()
TF1 * GetFitFunction ()
TGraph * GetErrorBand ()
TGraph * GetGraphFitFunction ()
Member functions (set)

int SetGraph (TGraphErrors *graph)
int SetFitFunction (TF1 *func)
Member functions (miscellaneous methods)

double LogAPrioriProbability (std::vector< double > parameters)
double LogLikelihood (std::vector< double > parameters)
double FitFunction (std::vector< double > x, std::vector< double > parameters)
int Fit ()
int Fit (TGraphErrors *graph, TF1 *func)
void DrawFit (const char *options="", bool flaglegend=false)
virtual double CDF (const std::vector< double > &parameters, int index, bool lower=false)

Private Attributes

TGraph * fErrorBand
TF1 * fFitFunction
TGraphErrors * fGraph
TGraph * fGraphFitFunction

Detailed Description

A class for fitting graphs with functions.

Author:
Daniel Kollar
Kevin Kröninger
Version:
1.0
Date:
2008 This class allows fitting of a TGraphErrors using a TF1 function. It doeasn't take the x uncertainties into account. For that look at BCGraphXFitter (not yet implemented).

Definition at line 34 of file BCGraphFitter.h.

Constructor & Destructor Documentation

BCGraphFitter::BCGraphFitter (  ) 

Default constructor

Definition at line 26 of file BCGraphFitter.cxx.

                             : BCModel("GraphFitter")
{
   fGraph = 0;
   fFitFunction = 0;
   fErrorBand = 0;
   fGraphFitFunction = 0;

   this -> MCMCSetNIterationsRun(2000);

   this -> SetFillErrorBand();
}

BCGraphFitter::BCGraphFitter ( TGraphErrors *  graph,
TF1 *  func 
)

Constructor

Parameters:
graph pointer to TGraphErrors
func pointer to TF1

Definition at line 40 of file BCGraphFitter.cxx.

                                                             : BCModel("GraphFitter")
{
   fGraph = 0;
   fFitFunction = 0;
   fErrorBand = 0;
   fGraphFitFunction = 0;

   this -> MCMCSetNIterationsRun(2000);

   this -> SetGraph(graph);
   this -> SetFitFunction(func);

   this -> SetFillErrorBand();
}

BCGraphFitter::~BCGraphFitter (  ) 

The default destructor.

Definition at line 175 of file BCGraphFitter.cxx.

{}

Member Function Documentation

double BCGraphFitter::CDF ( const std::vector< double > &  ,
int  ,
bool  = false 
) [virtual]

1dim cumulative distribution function of the probability to get the data f(x_i|param) for a single measurement, assumed to be of identical functional form for all measurements

Parameters:
parameters The parameter values at which point to compute the cdf
index The data point index starting at 0,1...N-1
lower only needed for discrete distributions! Return the CDF for the count one less than actually observed, e.g. in Poisson process, if 3 actually observed, then CDF(2) is returned

Reimplemented from BCModel.

Definition at line 329 of file BCGraphFitter.cxx.

                                                                                      {

   //format: x y error_x error_y
   std::vector<double> values = fDataSet->GetDataPoint(index)->GetValues();

   if (values.at(2))
      BCLog::OutWarning("BCGraphFitter::CDF: Non-zero errors in x-direction are ignored!");

   // get the observed value
   double yObs = values.at(1);

   // expectation value
   double yExp = FitFunction(values, parameters);

   return ROOT::Math::normal_cdf(yObs, values.at(3), yExp);
}

void BCGraphFitter::DrawFit ( const char *  options = "",
bool  flaglegend = false 
)

Draw the fit in the current pad.

Definition at line 278 of file BCGraphFitter.cxx.

{
   if (!fGraph)
   {
      BCLog::Out(BCLog::error, BCLog::error,"BCGraphFitter::DrawFit() : TGraphErrors not defined.");
      return;
   }

   if (!fFitFunction)
   {
      BCLog::Out(BCLog::error, BCLog::error,"BCGraphFitter::DrawFit() : Fit function not defined.");
      return;
   }

   // check wheather options contain "same"
   TString opt = options;
   opt.ToLower();

   // if not same, draw the histogram first to get the axes
   if(!opt.Contains("same"))
      fGraph -> Draw("ap");

   // draw the error band as central 68% probability interval
   fErrorBand = this -> GetErrorBandGraph(0.16, 0.84);
   fErrorBand -> Draw("f same");

   // draw the fit function on top
   fGraphFitFunction = this -> GetFitFunctionGraph( this->GetBestFitParameters() );
   fGraphFitFunction -> SetLineColor(kRed);
   fGraphFitFunction -> SetLineWidth(2);
   fGraphFitFunction -> Draw("l same");

   // now draw the histogram again since it was covered by the band and
   // the best fit
   fGraph -> Draw("p same");

   // draw legend
   if (flaglegend)
   {
      TLegend * legend = new TLegend(0.25, 0.75, 0.55, 0.95);
      legend -> SetBorderSize(0);
      legend -> SetFillColor(kWhite);
      legend -> AddEntry(fGraph, "Data", "P");
      legend -> AddEntry(fGraphFitFunction, "Best fit", "L");
      legend -> AddEntry(fErrorBand, "Error band", "F");
      legend -> Draw();
   }

   gPad -> RedrawAxis();
}

int BCGraphFitter::Fit ( TGraphErrors *  graph,
TF1 *  func 
)

Performs the fit of the graph with the function.

Parameters:
graph pointer to TGraphErrors object
func pointer to TF1 object
Returns:
An error code.

Definition at line 236 of file BCGraphFitter.cxx.

{
   // set graph
   if (!this -> SetGraph(graph))
      return 0;

   // set function
   if (!this -> SetFitFunction(func))
      return 0;

   // check setup
   BCLog::Out(BCLog::detail,BCLog::detail,
         Form("Fitting %d data points with function of %d parameters",GetNDataPoints(),GetNParameters()));
   if(GetNDataPoints() <= (int)GetNParameters())
   {
      BCLog::Out(BCLog::warning,BCLog::warning,
            Form("Number of parameters (%d) lower than or equal to number of points (%d)."
            , GetNParameters(), GetNDataPoints()));
      BCLog::Out(BCLog::warning,BCLog::warning,"Fit doesn't have much meaning.");
   }

   // perform marginalization
   this -> MarginalizeAll();

   // maximize posterior probability, using the best-fit values close
   // to the global maximum from the MCMC
   this -> FindModeMinuit( this -> GetBestFitParameters(), -1);

   // calculate p-value from the chi2 probability
   // this is only valid for a product of gaussiang which is the case for
   // the BCGraphFitter
   this -> GetPvalueFromChi2(this -> GetBestFitParameters(), 3);
   this -> GetPvalueFromChi2NDoF(this -> GetBestFitParameters(), 3);

   // print summary to screen
   this -> PrintShortFitSummary(1);

   return 1;
}

int BCGraphFitter::Fit (  )  [inline]

Performs the fit. The graph and the function has to beset beforehand.

Returns:
An error code.

Definition at line 117 of file BCGraphFitter.h.

         { return this -> Fit(fGraph, fFitFunction); };

double BCGraphFitter::FitFunction ( std::vector< double >  x,
std::vector< double >  parameters 
) [virtual]

Returns the value of the 1D fit function for a given set of parameters at a given x.

Parameters:
x point to calculate the function value at
parameters parameters of the function

Reimplemented from BCIntegrate.

Definition at line 226 of file BCGraphFitter.cxx.

{
   // set the parameters of the function
   fFitFunction -> SetParameters(&params[0]);

   return fFitFunction -> Eval(x[0]);
}

TGraph* BCGraphFitter::GetErrorBand (  )  [inline]
Returns:
pointer to the error band

Definition at line 72 of file BCGraphFitter.h.

         { return fErrorBand; };

TF1* BCGraphFitter::GetFitFunction (  )  [inline]
Returns:
pointer to TF1

Definition at line 67 of file BCGraphFitter.h.

         { return fFitFunction; };

TGraphErrors* BCGraphFitter::GetGraph (  )  [inline]
Returns:
pointer to TGraphErrors

Definition at line 62 of file BCGraphFitter.h.

         { return fGraph; };

TGraph* BCGraphFitter::GetGraphFitFunction (  )  [inline]
Returns:
pointer to a graph for the fit function

Definition at line 77 of file BCGraphFitter.h.

         { return fGraphFitFunction; };

double BCGraphFitter::LogAPrioriProbability ( std::vector< double >  parameters  )  [virtual]

The log of the prior probability. It is set to be flat in all parameters.

Parameters:
parameters vector containing the parameter values

Reimplemented from BCModel.

Definition at line 180 of file BCGraphFitter.cxx.

{
   // using flat probability in all parameters
   double logprob = 0.;
   for(unsigned int i=0; i < this -> GetNParameters(); i++)
      logprob -= log(this -> GetParameter(i) -> GetRangeWidth());

   return logprob;
}

double BCGraphFitter::LogLikelihood ( std::vector< double >  parameters  )  [virtual]

The log of the conditional probability.

Parameters:
parameters vector containing the parameter values

Reimplemented from BCModel.

Definition at line 192 of file BCGraphFitter.cxx.

{
   // initialize probability
   double logl = 0.;

   // set the parameters of the function
   // passing the pointer to first element of the vector is
   // not completely safe as there might be an implementation where
   // the vector elements are not stored consecutively in memory.
   // however it is much faster than copying the contents, especially
   // for large number of parameters
   fFitFunction -> SetParameters(&params[0]);

   // loop over all data points
   for (int i = 0; i < this -> GetNDataPoints(); i++)
   {
      std::vector <double> x = GetDataPoint(i) -> GetValues();

      // her we ignore the errors on x even when they're available
      // i.e. we treat them just as the region specifiers
      double y = x[1];
      double yerr = x[3];
      double yexp = this -> FitFunction(x,params);

      // calculate log of probability assuming
      // a Gaussian distribution for each point
      logl += BCMath::LogGaus(y, yexp, yerr, true);
   }

   return logl;
}

int BCGraphFitter::SetFitFunction ( TF1 *  func  ) 
Parameters:
func pointer to TF1 object

Definition at line 135 of file BCGraphFitter.cxx.

{
   if(!func)
   {
      BCLog::Out(BCLog::error,BCLog::error,"BCGraphFitter::SetFitFunction() : TF1 not created.");
      return 0;
   }

   // get the new number of parameters
   int npar = func -> GetNpar();
   if(!npar)
   {
      BCLog::Out(BCLog::error,BCLog::error,"BCGraphFitter::SetFitFunction() : TF1 has zero parameters. Not able to fit.");
      return 0;
   }

   // set the function
   fFitFunction = func;

   // update the model name to contain the function name
   this -> SetName(TString::Format("GraphFitter with %s",fFitFunction->GetName()));

   // reset parameters
   fParameterSet -> clear();

   // add parameters
   for (int i = 0; i < npar; ++i)
   {
      double xmin;
      double xmax;
      fFitFunction -> GetParLimits(i, xmin, xmax);

      this -> AddParameter(fFitFunction->GetParName(i), xmin, xmax);
   }

   return this -> GetNParameters();
}

int BCGraphFitter::SetGraph ( TGraphErrors *  graph  ) 
Parameters:
graph pointer to TGraphErrors object

Definition at line 57 of file BCGraphFitter.cxx.

{
   if(!graph)
   {
      BCLog::Out(BCLog::error,BCLog::error,"BCGraphFitter::SetGraph() : TGraphErrors not created.");
      return 0;
   }

   int npoints = graph -> GetN();
   if(!npoints)
   {
      BCLog::Out(BCLog::error,BCLog::error,"BCGraphFitter::SetGraph() : TGraphErrors is empty.");
      return 0;
   }
   else if(npoints==1)
   {
      BCLog::Out(BCLog::error,BCLog::error,"BCGraphFitter::SetGraph() : TGraphErrors has only one point. Not able to fit.");
      return 0;
   }

   fGraph = graph;

   double * x = fGraph -> GetX();
   double * y = fGraph -> GetY();
   double * ex = fGraph -> GetEX();
   double * ey = fGraph -> GetEY();

   if(!ey)
   {
      BCLog::Out(BCLog::error,BCLog::error,"BCGraphFitter::SetGraph() : TGraphErrors has NO errors set on Y. Not able to fit.");
      return 0;
   }

   BCDataSet * ds = new BCDataSet();

   // fill the dataset
   // find x and y boundaries for the error band calculation
   double xmin=x[0];
   double xmax=x[0];
   double ymin=y[0];
   double ymax=y[0];
   for (int i = 0; i < npoints; ++i)
   {
      // if x errors are not set, set them to zero
      double errx = ex ? ex[i] : 0.;

      // create the data point
      BCDataPoint * dp = new BCDataPoint(4);
      dp -> SetValue(0, x[i]);
      dp -> SetValue(1, y[i]);
      dp -> SetValue(2, errx);
      dp -> SetValue(3, ey[i]);
      ds -> AddDataPoint(dp);

      if(x[i]-errx < xmin)
         xmin = x[i]-errx;
      else if(x[i]+errx > xmax)
         xmax = x[i]+errx;

      if(y[i] - 5.*ey[i] < ymin)
         ymin = y[i] - 5.*ey[i];
      else if(y[i] + 5.*ey[i] > ymax)
         ymax = y[i] + 5.*ey[i];
   }

   this -> SetDataSet(ds);

   // set boundaries for the error band calculation
   this -> SetDataBoundaries(0, xmin, xmax);
   this -> SetDataBoundaries(1, ymin, ymax);

   this -> SetFitFunctionIndices(0, 1);

   return this -> GetNDataPoints();
}

Member Data Documentation

TGraph* BCGraphFitter::fErrorBand [private]

Pointer to the error band (for legend)

Definition at line 147 of file BCGraphFitter.h.

TF1* BCGraphFitter::fFitFunction [private]

The fit function

Definition at line 143 of file BCGraphFitter.h.

TGraphErrors* BCGraphFitter::fGraph [private]

The graph containing the data.

Definition at line 139 of file BCGraphFitter.h.

TGraph* BCGraphFitter::fGraphFitFunction [private]

Pointer to a graph for displaying the fit function

Definition at line 151 of file BCGraphFitter.h.

The documentation for this class was generated from the following files:
Generated on Mon Aug 30 2010 22:14:55 for Bayesian Analysis Toolkit by  doxygen 1.7.1