This C++ version of BAT is still being maintained, but addition of new features is unlikely. Check out our new incarnation, BAT.jl, the Bayesian analysis toolkit in Julia. In addition to Metropolis-Hastings sampling, BAT.jl supports Hamiltonian Monte Carlo (HMC) with automatic differentiation, automatic prior-based parameter space transformations, and much more. See the BAT.jl documentation.

Results of performance testing for BAT version 0.9

Back to | overview for 0.9 | all versions |

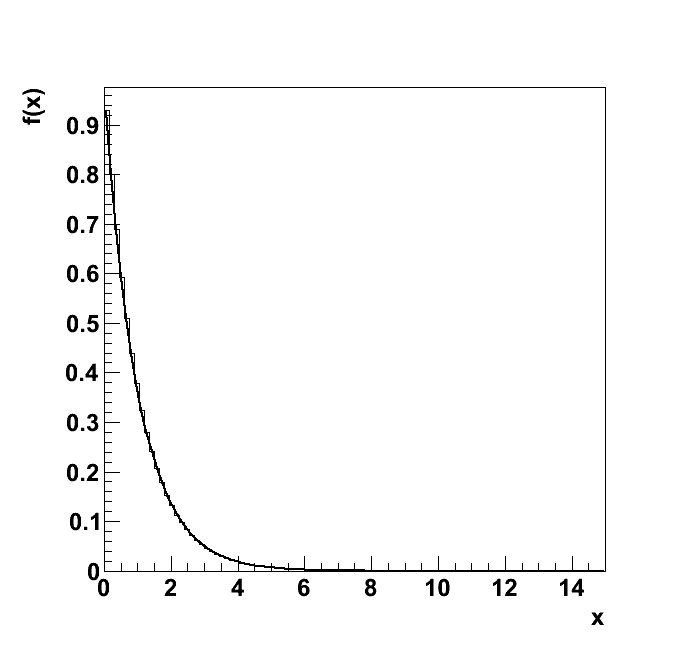
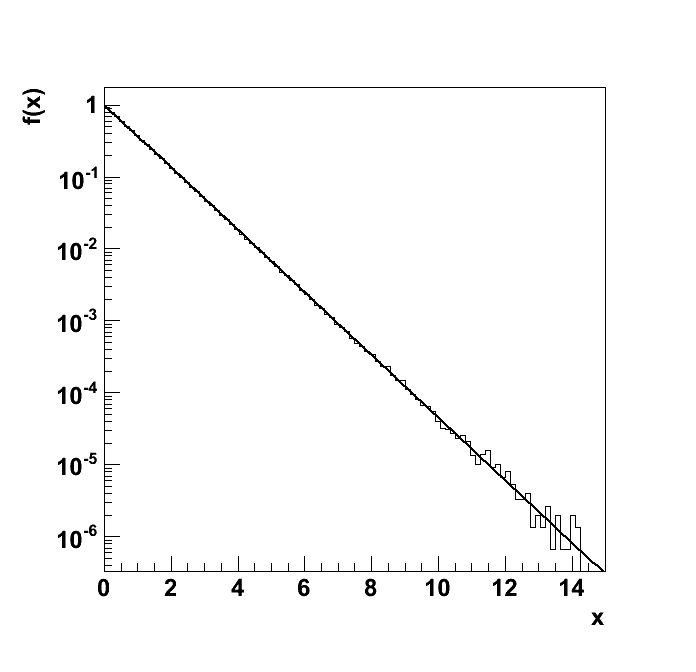
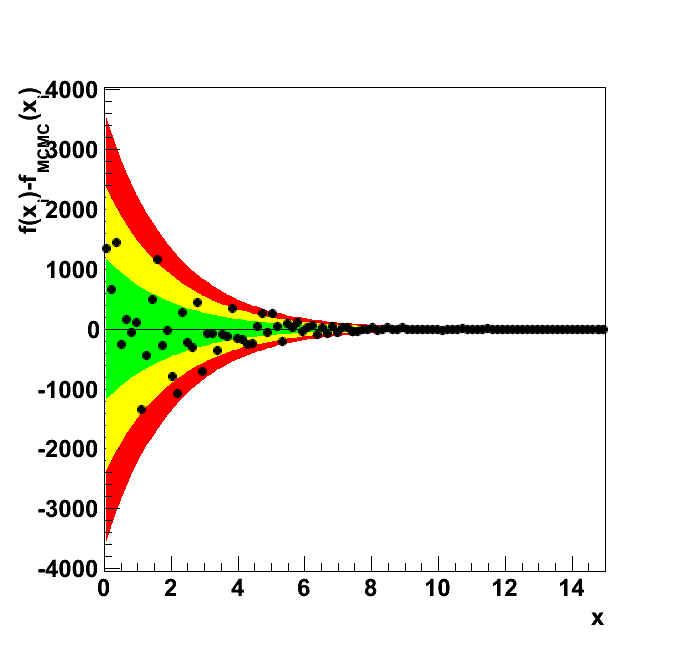
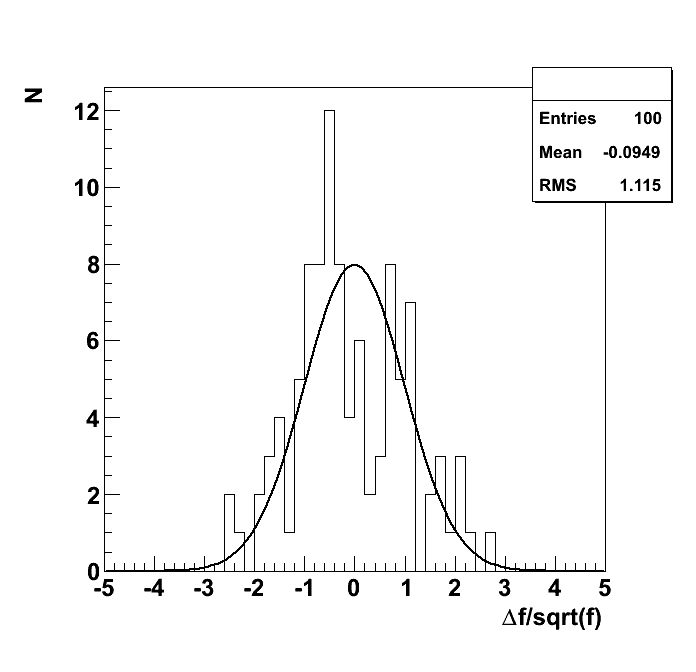
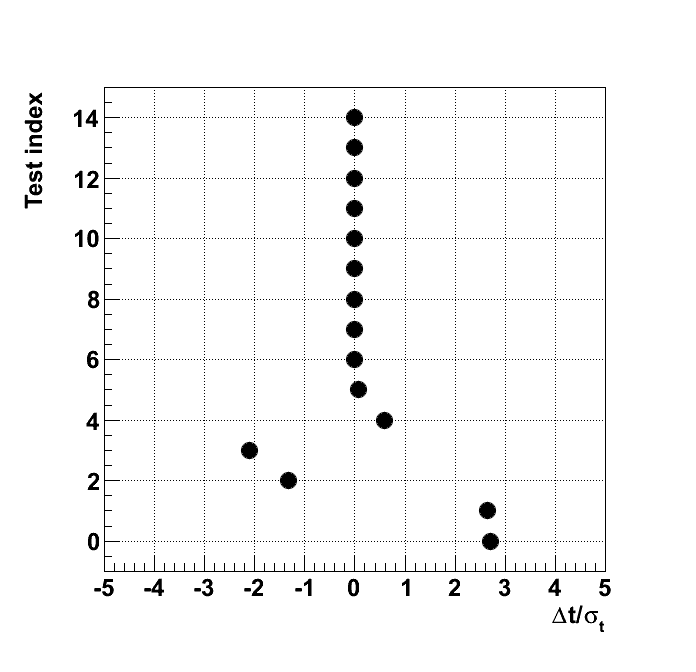
Test "1d_poisson_0"

Results
Status good
CPU time 19.01 s
Real time 19.23 s
Plots 1d_poisson_0.ps
Log 1d_poisson_0.log

Settings
N chains 10
N lag 10
Convergence true
N iterations (pre-run) 4000
N iterations (run) 10000000

Plots
Auto-correlation for the parameter.Distribution from MCMC and analytic function.Distribution from MCMC and analytic function in log-scale.
Difference between the distribution from MCMC and the analytic function. The one, two and three sigma uncertainty bands are colored green, yellow and red, respectively.Pull between the distribution from MCMC and the analytic function. The Gaussian has a mean value of 0 and a standard deviation of 1 (not fitted).Summary of subtest values.

Subtest Status Target Test Uncertainty Deviation [%] Deviation [sigma] Tol. (Good) Tol. (Acceptable) Tol. (Bad)
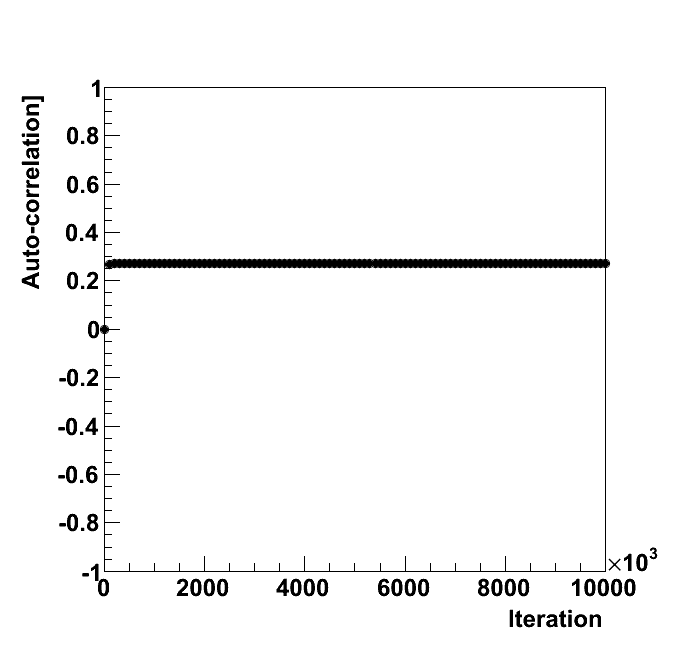
correlation par 0 off 0 0.2714 0.0269 - -10.09 0.3 0.5 0.7
chi2 good 79 112.3 12.57 42.12 -2.647 37.71 62.85 87.99
KS good 1 0.5821 0.95 -41.79 0.4399 0.95 0.99 0.9999
mean good 1 0.9993 0.0003164 -0.06685 2.113 0.0009493 0.001582 0.002215
mode good 0 0.075 0.1291 - -0.5809 0.3873 0.6455 0.9037
variance good 0.9999 1.02 0.2829 1.964 -0.0694 0.8488 1.415 1.98
quantile10 good 0.1077 0.1076 0.1291 -0.09678 0.0008073 0.3873 0.6455 0.9037
quantile20 good 0.226 0.2257 0.1291 -0.09345 0.001636 0.3873 0.6455 0.9037
quantile30 good 0.3593 0.359 0.1291 -0.1048 0.002918 0.3873 0.6455 0.9037
quantile40 good 0.5135 0.513 0.1291 -0.1108 0.004408 0.3873 0.6455 0.9037
quantile50 good 0.6958 0.6951 0.1291 -0.09389 0.00506 0.3873 0.6455 0.9037
quantile60 good 0.9174 0.9165 0.1291 -0.09643 0.006852 0.3873 0.6455 0.9037
quantile70 good 1.204 1.204 0.1291 -0.06181 0.005766 0.3873 0.6455 0.9037
quantile80 good 1.612 1.61 0.1291 -0.09002 0.01124 0.3873 0.6455 0.9037
quantile90 good 2.305 2.304 0.1291 -0.05587 0.009977 0.3873 0.6455 0.9037

Subtest Description
correlation par 0 Calculate the auto-correlation among the points.
chi2 Calculate χ2 and compare with prediction for dof=number of bins with an expectation >= 10.
Tolerance good: |χ2-E[χ2]| < 3 · (2 dof)1/2,
Tolerance acceptable: |χ2-E[χ2]| < 5 · (2 dof)1/2,
Tolerance bad: |χ2-E[χ2]| < 7 · (2 dof)1/2.
KS Calculate the Kolmogorov-Smirnov probability based on the ROOT implemention.
Tolerance good: KS prob > 0.05,
Tolerance acceptable: KS prob > 0.01
Tolerance bad: KS prob > 0.0001.
mean Compare sample mean, <x>, with expectation value of function, E[x].
Tolerance good: |<x> -E[x]| < 3 · (V[x]/n)1/2,
Tolerance acceptable: |<x> -E[x]| < 5 · (V[x]/n)1/2,
Tolerance bad: |<x> -E[x]| < 7 · (V[x]/n)1/2.
mode Compare mode of distribution with mode of the analytic function.
Tolerance good: |x*-mode| < 3 · V[mode]1/2,
Tolerance acceptable: |x*-mode| < 5 · V[mode]1/2 bin widths,
Tolerance bad: |x*-mode| < 7 · V[mode]1/2.
variance Compare sample variance s2 of distribution with variance of function.
Tolerance good: 3 · V[s2]1/2,
Tolerance acceptable: 5 · V[s2]1/2,
Tolerance bad: 7 · V[s2]1/2.
quantile10 Compare quantile of distribution from MCMC with the quantile of analytic function.
Tolerance good: |q_{X}-E[q_{X}]|<3·V[q]1/2,
Tolerance acceptable: |q_{X}-E[q_{X}]|<5·V[q]1/2,
Tolerance bad: |q_{X}-E[q_{X}]|<7·V[q]1/2.
quantile20 Compare quantile of distribution from MCMC with the quantile of analytic function.
Tolerance good: |q_{X}-E[q_{X}]|<3·V[q]1/2,
Tolerance acceptable: |q_{X}-E[q_{X}]|<5·V[q]1/2,
Tolerance bad: |q_{X}-E[q_{X}]|<7·V[q]1/2.
quantile30 Compare quantile of distribution from MCMC with the quantile of analytic function.
Tolerance good: |q_{X}-E[q_{X}]|<3·V[q]1/2,
Tolerance acceptable: |q_{X}-E[q_{X}]|<5·V[q]1/2,
Tolerance bad: |q_{X}-E[q_{X}]|<7·V[q]1/2.
quantile40 Compare quantile of distribution from MCMC with the quantile of analytic function.
Tolerance good: |q_{X}-E[q_{X}]|<3·V[q]1/2,
Tolerance acceptable: |q_{X}-E[q_{X}]|<5·V[q]1/2,
Tolerance bad: |q_{X}-E[q_{X}]|<7·V[q]1/2.
quantile50 Compare quantile of distribution from MCMC with the quantile of analytic function.
Tolerance good: |q_{X}-E[q_{X}]|<3·V[q]1/2,
Tolerance acceptable: |q_{X}-E[q_{X}]|<5·V[q]1/2,
Tolerance bad: |q_{X}-E[q_{X}]|<7·V[q]1/2.
quantile60 Compare quantile of distribution from MCMC with the quantile of analytic function.
Tolerance good: |q_{X}-E[q_{X}]|<3·V[q]1/2,
Tolerance acceptable: |q_{X}-E[q_{X}]|<5·V[q]1/2,
Tolerance bad: |q_{X}-E[q_{X}]|<7·V[q]1/2.
quantile70 Compare quantile of distribution from MCMC with the quantile of analytic function.
Tolerance good: |q_{X}-E[q_{X}]|<3·V[q]1/2,
Tolerance acceptable: |q_{X}-E[q_{X}]|<5·V[q]1/2,
Tolerance bad: |q_{X}-E[q_{X}]|<7·V[q]1/2.
quantile80 Compare quantile of distribution from MCMC with the quantile of analytic function.
Tolerance good: |q_{X}-E[q_{X}]|<3·V[q]1/2,
Tolerance acceptable: |q_{X}-E[q_{X}]|<5·V[q]1/2,
Tolerance bad: |q_{X}-E[q_{X}]|<7·V[q]1/2.
quantile90 Compare quantile of distribution from MCMC with the quantile of analytic function.
Tolerance good: |q_{X}-E[q_{X}]|<3·V[q]1/2,
Tolerance acceptable: |q_{X}-E[q_{X}]|<5·V[q]1/2,
Tolerance bad: |q_{X}-E[q_{X}]|<7·V[q]1/2.